This article allows the reader to interactively manipulate components of a vector and observe the changes in the cordinate direction angles. It is my hope that it may provide an intuition about coordinate direction angles.

Cartesian vectors recap

A vector $$\mathbf{A}$$ can be represented in cartesian form as: \mathbf{A} = A_{x}\mathbf{i} + A_{y}\mathbf{j} + A_{z}\mathbf{k}, where $$A_x$$, $$A_y$$, and $$A_z$$ are the $$x$$, $$y$$, and $$z$$ components of the vector. We can also calculate a vector's magnitude using the following equation A = \sqrt{A_{x}^2 + A_{y}^2 + A_{z}^2}.

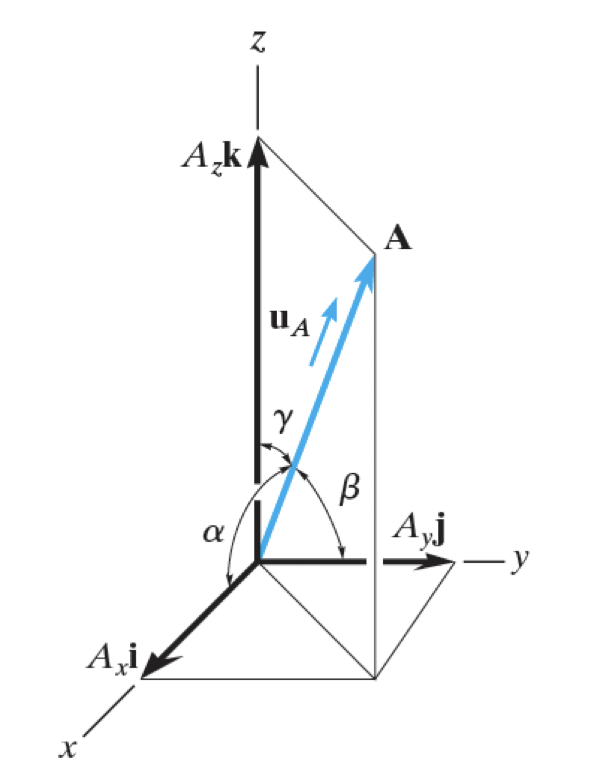
Coordinate direction angles

The direction of $$\mathbf{A}$$ can be defined by the coordinate direction angles $$\alpha$$, $$\beta$$ and $$\gamma$$, measured between the tail of $$\mathbf{A}$$ and the positive $$x$$, $$y$$, $$z$$ axes. Figure 2-26 in the textbook ilustrates this idea:

Figure 2-26, taken from the Engineering Mechanics: Statics textbook by R.C. Hibbeler.

To calculate the coordinate direction angles, we first obtain the directional cosines. \cos(\alpha) = \frac{A_x}{A}, \:\: \cos(\beta) = \frac{A_y}{A}, \:\: \cos(\gamma) = \frac{A_z}{A}. Then we can take the inverse cosines to determine the angle.

Let us now try and build an intuition about these coordinate direction angles, and how it relates to the components of a vector. The interactive diagram below plots a vector $$\mathbf{F}$$, and the planes in which the coordinate direction angles live. In the legend you will see the cartesian representation of $$\mathbf{F}$$, along with values for $$\alpha$$, $$\beta$$ and $$\gamma$$, rounded to the nearest integer. Try adjusting the components of $$\mathbf{F}$$ by moving the sliders and observe how the coordinate direction angles change in response. You can also pan the diagram to visualise the planes from different perspectives. Here are some things to think about:

1. When is $$ 0 < \alpha < 90$$ and when is $$ 90 < \alpha < 180$$?
2. What about $$\alpha=0, 90, 180$$? Do the same for $$\beta$$ and $$\gamma$$.
3. Try to find a case where $$\alpha$$ remains fixed while changing the $$y$$ and $$z$$ components of $$\mathbf{F}$$. Why does this happen?
4. For some practice, try to calculate the coordinate direction angles yourself, rounded to the nearest integer.

adjust value $$x$$

adjust value $$y$$

adjust value $$z$$

You may notice that the head of the vector has a dot instead of an arrow. This is a limitation of the library used.